Apr 01, 17 · Use suitable identities to find the following products (i) (x 4) (x 10) (ii) (x 8) (x – 10) (iii) (3x 4) (3x – 5) (iv) (y 2 3 / 2) (y 2 – 3 / 2) (vIn the algebraic identities for class 9, we will cover all the identities mentioned in the CBSE class 9 (NCERT) syllabus These algebraic identities basically carry variable equations in such a way, that the Lefthand side (LHS) of the equation is equal to its Righthand side(RHS)Access TopperLearning's free Selina Solutions for ICSE Class 9 Mathematics Chapter 4 Expansion to learn about finding the square of a given algebraic expression using expansion Also, go through the solutions to understand expansion of cubes Highlyexperienced Maths experts have created the answers for textbook exercises in a stepwise format to help it easy for students to

Ex 2 5 1 Class 9 Polynomials Use Suitable Identities To Find
Expand x 2 y 4 z whole square using suitable identity
Expand x 2 y 4 z whole square using suitable identity-∇2f(x,y,z) = 02∇(xy z)·∇(x−2z) = 2(ij k)·(i−2k) = 2(10−2) = −2 This example may be checked by expanding (x y z)(x − 2z) and directly calculating the Laplacian Exercise 4 Use this rule to calculate the Laplacian of the scalar fields given below (click onCoefficient of x 2 y 2 z 2 in the term –4x 2 y 2 z 2 is –4 Coefficient of z 2 in the term z 2 is 1 Use a suitable identity to get each of the following products (i) (x 3)(x 3) Squares and Square Roots;



Factoring Using The Difference Of Squares Pattern Video Khan Academy
Free Maclaurin Series calculator Find the Maclaurin series representation of functions stepbystepEx 25 Class 9 Maths Question 1 Use suitable identities to find the following products (i) (x4)(x10) Ex 25 Class 9 Maths Question 4 Expand each of the following, using suitable identities (i) (x 2y 4z) 2 (ii) (2x y z) 2 (x y z)x 2 y 2 – 2xy y 2 z 22yz z 2 x 2 – 2zx = (x y z)(xy)Free expand & simplify calculator Expand and simplify equations stepbystep This website uses cookies to ensure you get the best experience By using this
112 Examples The standard inner product is hx;yi= xTy= X x iy i;Apr 18, 21 Algebraic Identities Polynomials, Class 9, Mathematics EduRev Notes is made by best teachers of Class 9 This document is highly rated byApr 24, 19 · NCERT Exemplar Solutions We hope the NCERT Exemplar Class 8 Maths Chapter 7 Algebraic Expressions, Identities and Factorisation help you If you have any query regarding NCERT Exemplar Class 8 Maths Chapter 7 Algebraic Expressions, Identities and Factorisation, drop a comment below and we will get back to you at the earliest
Dec 07, · Example 11 If a b c = 9 and ab bc ca = 40, find a 2 b 2 c 2 Solution We know that Example 12 If a 2 b 2 c 2 = 250 and ab bc ca = 3, find a b c Solution We know that Example 13 Write each of the following in expanded form (i) (2x 3y) 3 (ii) (3x – 2y) 3 Solution Example 14 If x y = 12 and xy = 27, find the value of x 3 y 3Example 2 if x = 10 and y is 4 (10 4) 2 = 10 2 2·10·4 4 2 = 100 80 16 = 36 The opposite is also true 25 a 4a 2 = 5 2 2·2·5 (2a) 2 = (5 2a) 2 Consequences of the above formulasX;y2R n The standard inner product between matrices is hX;Yi= Tr(XTY) = X i X j X ijY ij where X;Y 2Rm n Notation Here, Rm nis the space of real m nmatricesTr(Z) is the trace of a real square



Expand Using The Identity A 2x 3y Z 2 Brainly In
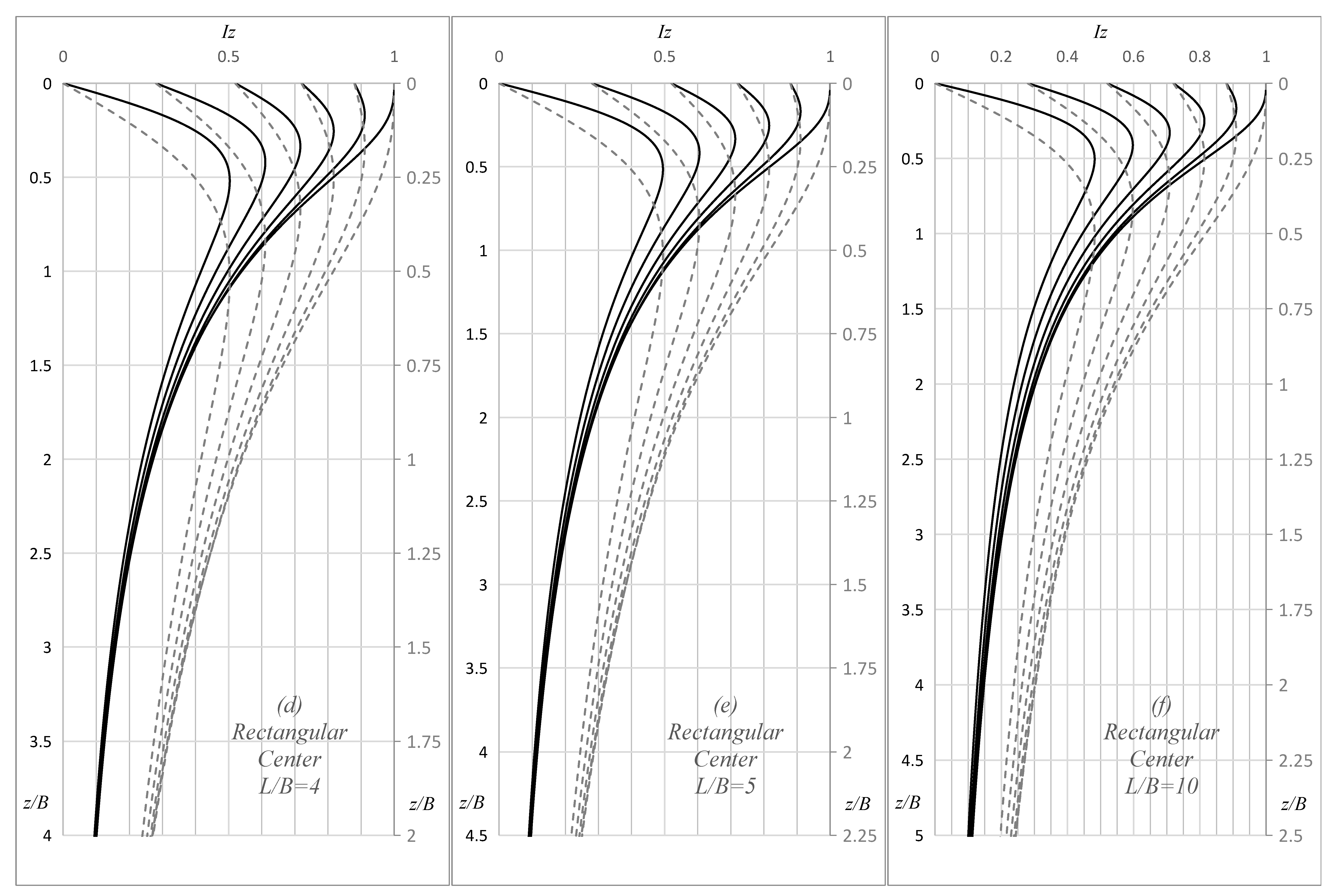


Applied Sciences Free Full Text Strain Influence Factor Charts For Settlement Evaluation Of Spread Foundations Based On The Stress Strain Method Html
Now since z 1 ⁄ 2 e 1 ⁄ 2 Log z, on the contour outside the branch cut, we have gained 2 π in argument along γ (By Euler's identity, e iπ represents the unit vector, which therefore has π as its log This π is what is meant by the argument of z The coefficient of 1 / 2 forces us to use 2 π) SoIn mathematics, a formal power series is a generalization of a polynomial, where the number of terms is allowed to be infinite, with no requirements of convergenceThus, the series may no longer represent a function of its variable, merely a formal sequence of coefficients, in contrast to a power series, which defines a function by taking numerical values for the variable within a radius of4 Binomial Expansions 41 Pascal's riTangle The expansion of (ax)2 is (ax)2 = a2 2axx2 Hence, (ax)3 = (ax)(ax)2 = (ax)(a2 2axx2) = a3 (12)a 2x(21)ax x 3= a3 3a2x3ax2 x urther,F (ax)4 = (ax)(ax)4 = (ax)(a3 3a2x3ax2 x3) = a4 (13)a3x(33)a2x2 (31)ax3 x4 = a4 4a3x6a2x2 4ax3 x4 In general we see that the coe cients of (a x)n



Ex 2 5 1 Class 9 Polynomials Use Suitable Identities To Find



Ex 2 5 4 Expand Each Of The Following Using Suitable
Click here👆to get an answer to your question ️ Expand ( 2x 5y 3z )^2 using suitable identitiesA 2 b 2 c 2 118 – 118 = 625 – 118 subtracting 118 from both the sides Therefore, a 2 b 2 c 2 = 507 Thus, the formula of square of a trinomial will help us to expand 7th Grade Math Problems 8th Grade Math Practice From Square of a Trinomial to HOME PAGE(z2 4)2 = 1 (z 2i)2(z 2i)2 Let f(z) = 1 (z 2i)2 Clearly f(z) is analytic inside C So, by Cauchy's formula for derivatives solution to the previous solution won't work because we can't nd an appropriate f(z) that is analytic on the whole interior of C Our solution is to split the curve into two pieces Notice that C 3 is



Use A Suitable Identity To Get Each Of The Following Products I



Expand Using Identity 3 X Minus 2 Y Z Whole Square Brainly In
Expand polynomial (x3)(x^35x2) GCD of x^42x^39x^246x16 with x^48x^325x^246x16;Jan 30, 18 · 2 answers Give possible expression for the length and breadth of the rectangle whose area is given by 4a2 4a 3 asked Jan 30, 18May 29, 18 · Transcript Example Expand (4a – 2b – 3c)2 (4a – 2b – 3c)2 = (4a (–2b) (–3c)) 2 Using (x y z)2 = x2 y2 z2 2xy 2yz 2zx Putting x = 4a



Theta Function Wikipedia



Analyzing Polynomial Identities Video Khan Academy
An algebraic identity is an equality that holds for any values of its variables For example, the identityExpand (2x 3y 2z)^2 Bajwa302 Bajwa302 Math It is used to calculate the whole square that has combine with terms to expand it for having right answered it It has to expand with suitable identities and carry out least numbers and expand it(x 4 – 1) = (x 2 1)((x) 2 –(1) 2) = (x 2 1)(x 1)(x – 1) Eample 3 Factorise 16x 2 4y 2 9z 2 – 16xy 12yz – 24zx using standard algebraic identities Solution 16x 2 4y 2 9z 2 – 16xy 12yz – 24zx is of the form Identity V



Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes


How Did Urban Land Expand In China Between 1992 And 15 A Multi Scale Landscape Analysis
Mar 16, 17 · Ex 25, 4 Expand each of the following, using suitable identities (x 2y 4z)2 (x 2y 4z)2 Using (a b c)2 = a2 b2 c2 2ab 2bc 2ac Where a = x , b = 2y, c = 4z = x2 (2y)2 (4z)2 2(x) (2y) 2(2y) (4z) 2 (4z) (x) = x2 4y2 16z2 4xy 16yz 8xz Ex 25, 4 Expand each of the following, using suitable identities (ii) (2x y z)2 (2x y z)2 = (2x ( y) z)2 Using (a b c)2 = a2 b2 c2 2ab 2bc 2ac Where a = 2x , b = y, c = z = (2x)2 (y)2 (z)2 2Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel knowledge andExpand the following product (3 x 1) (2 x 4) `(3x1)(2x4)` returns `3*x*2*x3*x*42*x4` Expand this algebraic expression `(x2)^3` returns `2^33*x*2^23*2*x^2x^3` Note that the result is not returned as the simplest expression in order to be able to follow the steps of calculations To simplify the results, simply use the reduce function



How To Expand Using The Identity A B C 2 B2 C2 2ab 2bc 2ca Youtube



Example 19 Write 3a 4b 5c 2 In Expanded Form Examples
Use convenient identities for simplification, specified as the commaseparated pair consisting of 'IgnoreAnalyticConstraints' and true or false Setting 'IgnoreAnalyticConstraints' to true can give you simpler solutions, which could lead to results not generally valid In other words, this option applies mathematical identities that are convenient, but the results might not hold for allSo we've got 3y squared plus 6x to the third we're raising this whole thing to the fifth power and we could clearly use a binomial theorem or Pascal's triangle in order to find the expansion of that but what I want to do really is a as an exercise is to try to hone in on just one of the terms and in particular I want to hone in on the term that has some coefficient times X to the sixth Y toAnd now solve the difference of two squares with a = 36 and b = 4y 2 Solution Factor the equation (rearranged) 36 − 4 y 2 using the identity a 2 − b 2 = ( a b) ( a − b) First factor out the GCF 4 ( 9 − y 2) Both terms are perfect squares so from a 2 b 2 we can find a and b



4x 5 Y 4 4x 5 3y 4 Brainly In



Rd Sharma Solutions For Class 8 Chapter 6 Algebraic Expressions And Identities Download Free Pdf
Binomial Theorem Formula The generalized formula for the patternExample 2 Solve (6m 9n) 2 Solution This proceeds as Given polynomial (6m 9n) 2 represents identity second ie (a b) 2 Where a = 6m and b = 9n Now apply values of a and b on the identity ie (a b) 2 = a 2 b 2 2ab and we get (6m 9n) 2 = (6m) 2 (9n) 2 2(6m)(9n) Expand the exponential forms and we get = 36m 2 81n 2 2(6mSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more
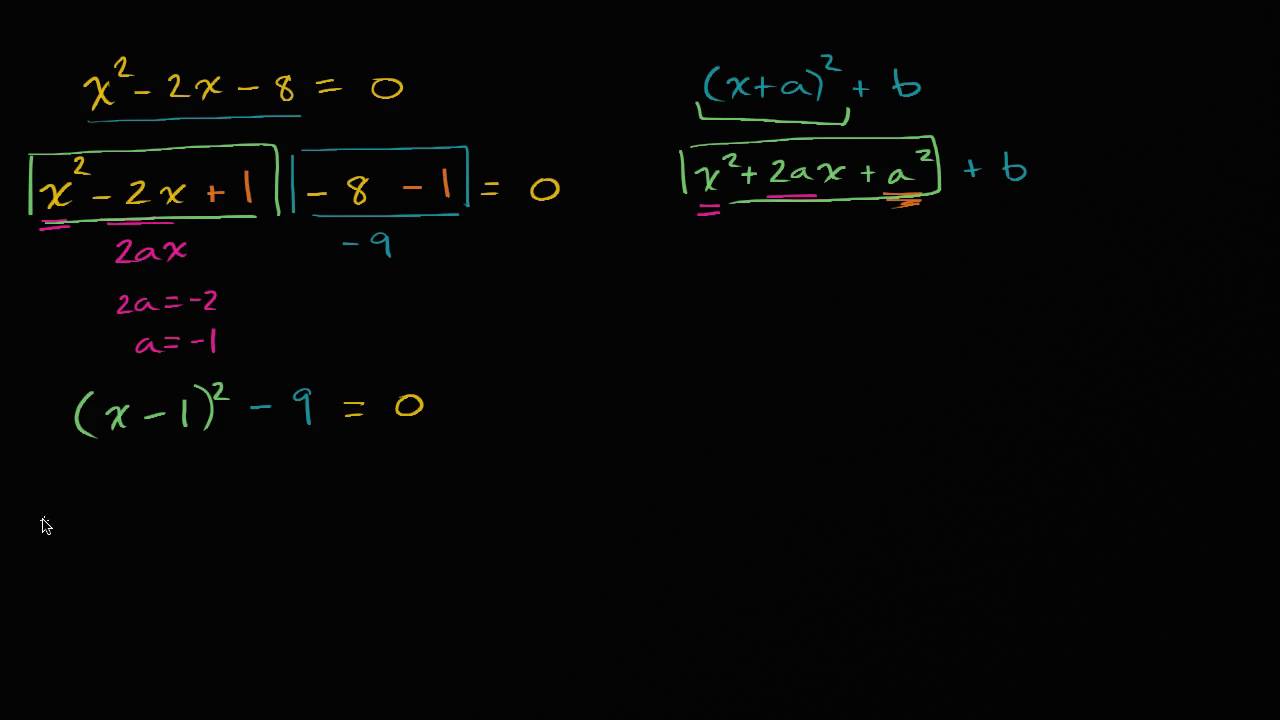


Worked Example Rewriting Solving Equations By Completing The Square Video Khan Academy



Ex 2 5 6 Write The Following Cubes In Expanded Form Ex 2 5
In other words, f(ˇ x) = f(x) If f(x) ˘ X1 k=1 b ksin(kx) is the Fourier sine series of f, prove that b k= 0 for even k (Hint write out the formula for b k and make the change of variables y= ˇ x) Solution Making the change of variables y= ˇ x, we get b k= 2 ˇ Z ˇ 0 f(x)sin(kx)dx = 2 ˇ ZJan 30, 18 · Using suitable identity, evaluate the following (i) 103 3 (ii) 101 x 102 (iii) 999 2 Firstly adjust the given number into two number such that one is a multiple of 10 and use the proper identitySymmetric with respect to the line x= ˇ=2;



Expand And Simplify Binomial Squares 2x 3y 2 Youtube



Ex 2 5 4 Expand Each Of The Following Using Suitable
Introduction to x plus y whole cube identity with example problems and proofs to learn how to derive xy whole cube formula in mathematicsHowever, for quite some time Pascal's Triangle had been well known as a way to expand binomials (Ironically enough, Pascal of the 17th century was not the first person to know about Pascal's 3 = x 3 3x 2 y 3xy 2 y 3 (x y) 4 = x 4 4x 3 y 6x 2 y 2 4xy 3 y 4;Enter your queries using plain English To avoid ambiguous queries, make sure to use parentheses where necessary Here are some examples illustrating how to ask about factoring factor quadratic x^27x12;



Expand The Following Expand 4 1 3x 3 Brainly In



Xyz 4 Xyz 2 Use Identity Brainly In
Expand each of the following using suitable identities X 2 Y 4 Z whole square Get the answers you need, now!X 2 y 2 z 2 = r 1 2 (x d) 2 y 2 z 2 = r 2 2 Subtracting the first equation from the second, expanding the powers, and solving for x gives x = d 2 r 2 2 r 1 2 / 2 d The intersection of the two spheres is a circle perpendicular to the x axis, at a position given by x above Substituting this into the equation of the firstThe last step uses identities to find the factors for the given expression Since the LHS for the identity a 2 2abb 2 is (ab) 2 we write the factors using the identity as (3x6) 2 = (3x6) (3x6) So the factor for 9x 2 –18 x 36 is (3x6) (3x6) Learn more about Factorisation using Division Solved Examples For You



Expand Each Of The Following Using Suitable Identities 2x 3y 2z 2



2a 3b Expand It Using Suitable Identities Brainly In
Quotient of x^38x^217x6 with x3Two numbers r and s sum up to 2 exactly when the average of the two numbers is \frac{1}{2}*2 = 1 You can also see that the midpoint of r and s corresponds to the axis of symmetry of the parabola represented by the quadratic equation y=x^2BxCA complex number z = x yi will lie on the unit circle when x 2 y 2 = 1 Some examples, besides 1, –1, i, and –1 are ±√2/2 ± i√2/2, where the pluses and minuses can be taken in any order They are the four points at the intersections of the diagonal lines y = x and y = x with the unit circle We'll see them later as square roots of
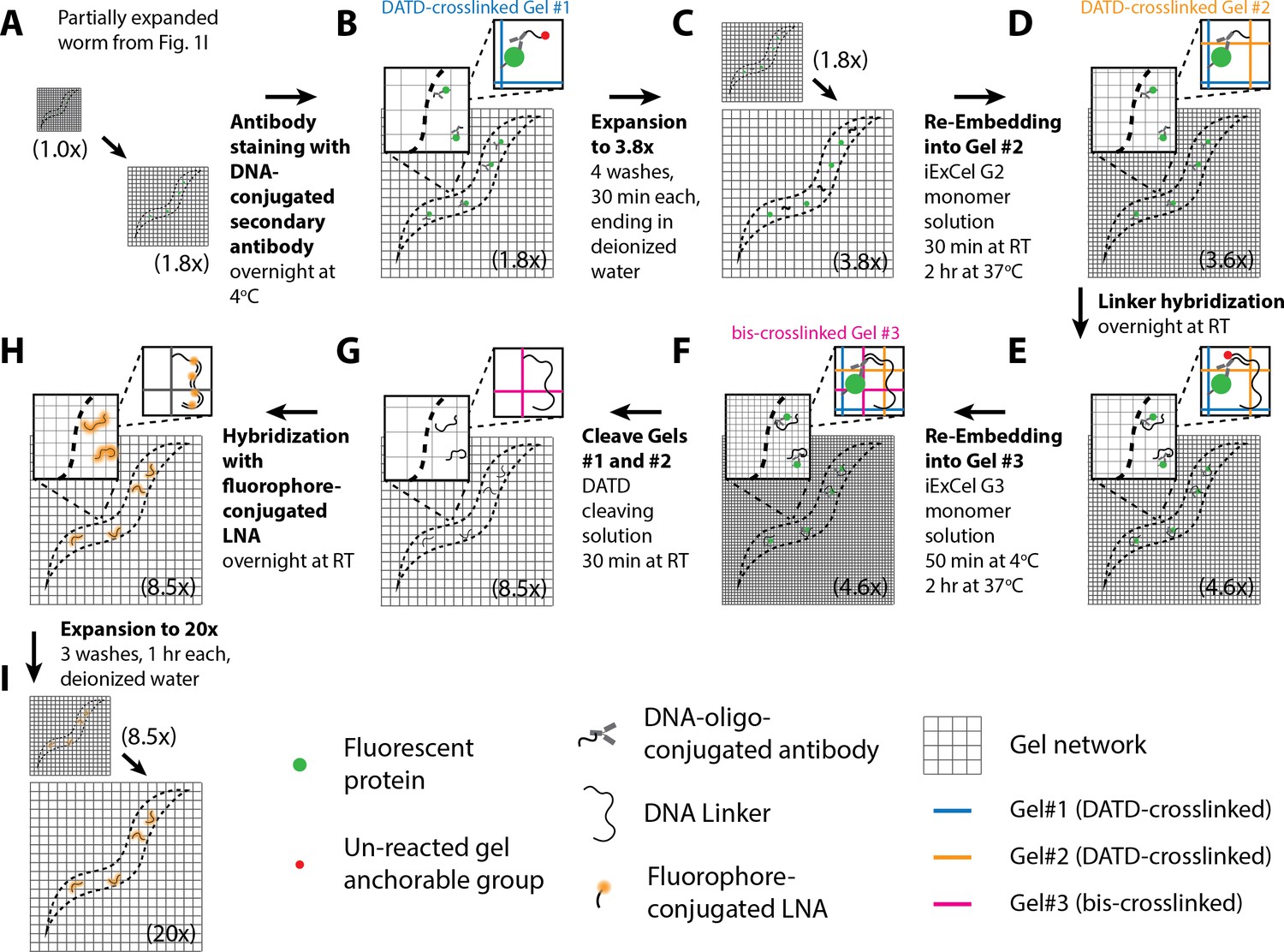


Figures And Data In Expansion Microscopy Of C Elegans Elife



Find The Product X Y Z X 2 Y 2 Z 2 Xy Yz Zx Youtube
Factorization of x 3 y 3 It can be seen in most book that x 3 y 3 can be factorized by dividing the expression by (x y) After division we get a quotient of (x 2 xy y 2) with no remainder Therefore However, this method involves knowing the factor (x y) beforehand (and the understanding of Factor Theorem)6041/6431 Spring 08 Quiz 2 Wednesday, April 16, 730 930 PM SOLUTIONS Name Recitation Instructor TA Question PartExpand the following (2xyz)the whole raised to 2 Share with your friends Share 0



Using A Suitable Identity Evaluate 105 2
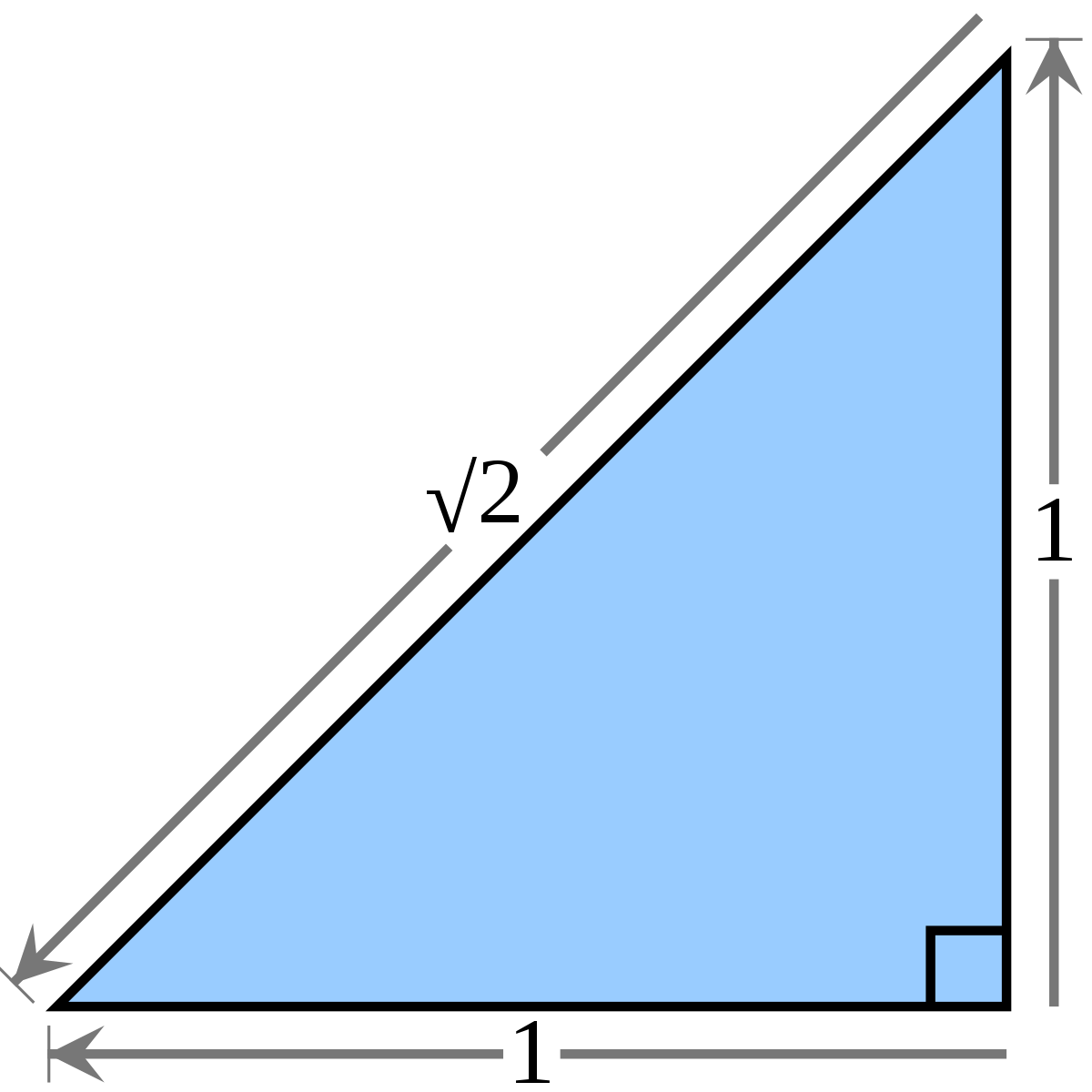


Square Root Of 2 Wikipedia
Expand following, using suitable identities (x 2y 4z)^2 CBSE CBSE Class 9 Textbook Solutions 50 Important Solutions 1 Question Bank Solutions 8008 Concept Notes & Videos 287 Syllabus Advertisement Remove all ads Expand following, using suitable identities (x 2y 4z)^2 MathematicsChapter 13 Visualizing Solid Shapes;The perfect cube forms
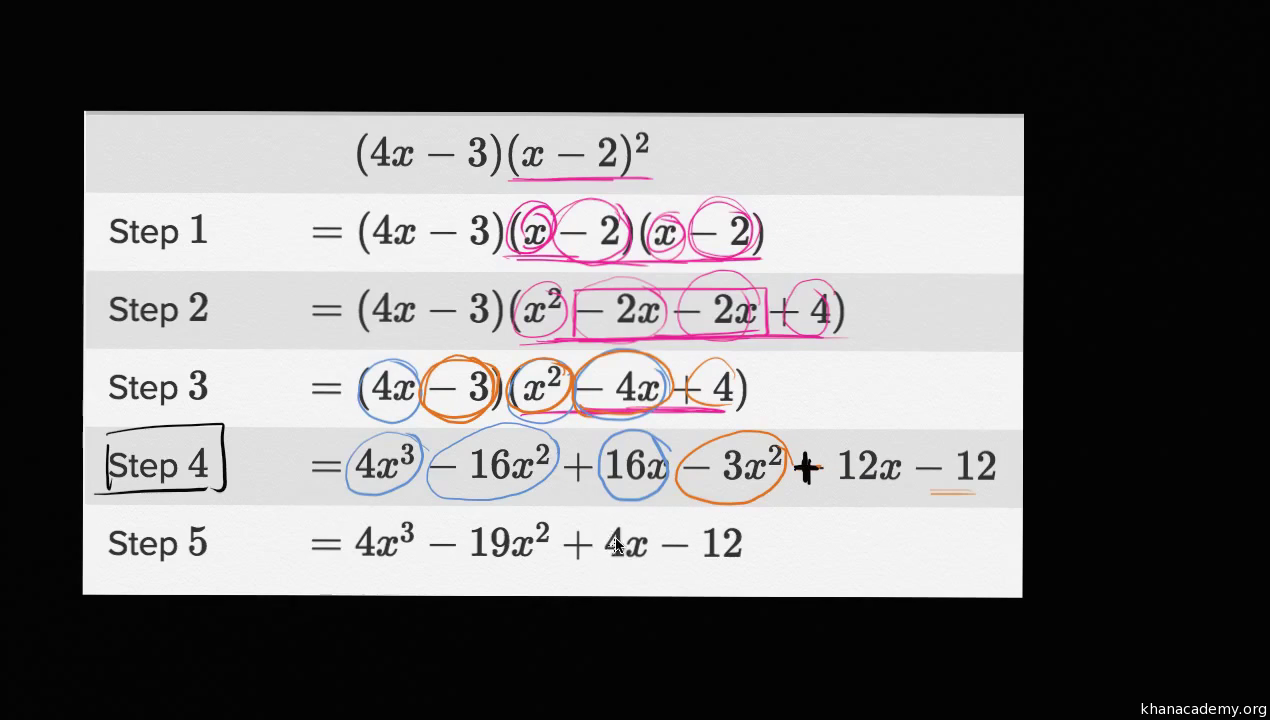


Analyzing Polynomial Identities Video Khan Academy



Factoring Using The Difference Of Squares Pattern Video Khan Academy
= (x 2 1/x 2) 2 since a = x 2 and b = 1/x 2 In the 2nd identity, a 2 2ab b 2 = (a b) 2 , 1st and the last term should be perfect square and the middle term is two times the square root of 1st and the last term and the sign of the middle term is negative



Square Algebra Wikipedia



Expand And Simplify Binomial Squares 2x 3y 2 Youtube



Combinators And The Story Of Computation Stephen Wolfram Writings



Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes



Scalable And Isotropic Expansion Of Tissues With Simply Tunable Expansion Ratio Park 19 Advanced Science Wiley Online Library



Expand 1 4a 1 2b 1 Whole Square Brainly In
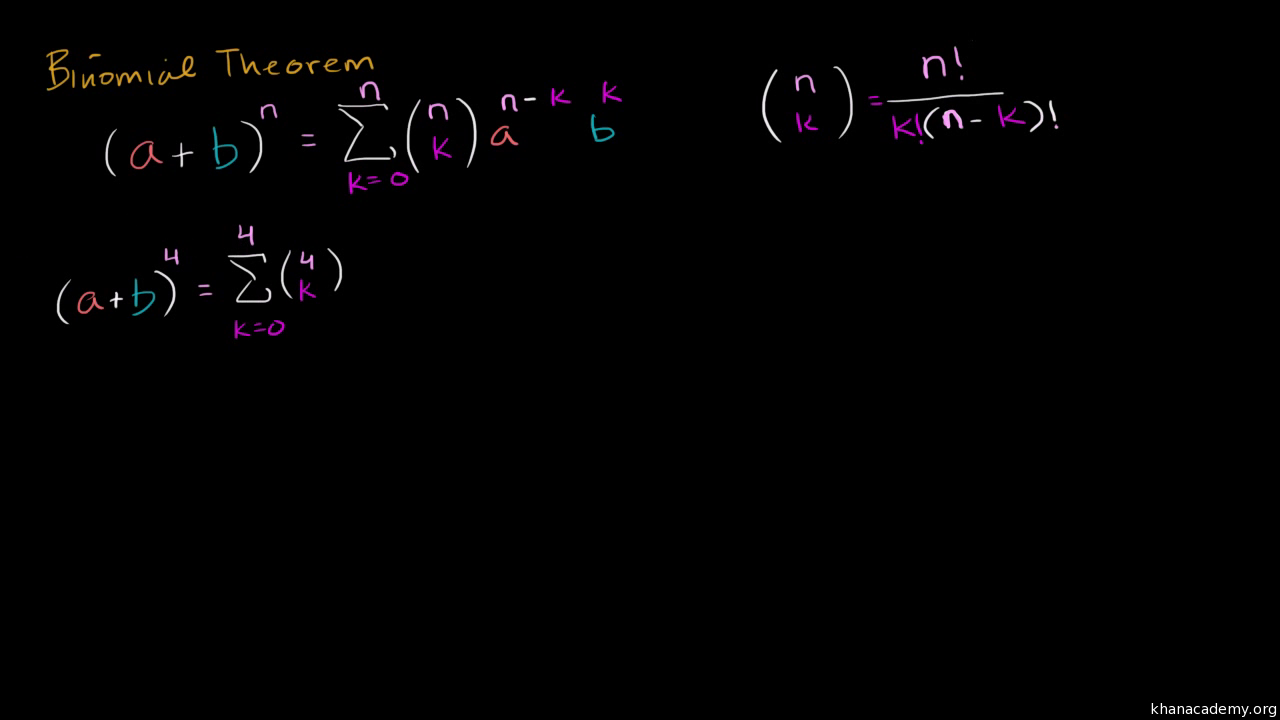


Intro To The Binomial Theorem Video Khan Academy



Expand Using Identities 3x 5y 2



Solve Using Suitable Identity X 3y X 3xy 9y Brainly In



A Bayesian Framework For Multiple Trait Colocalization From Summary Association Statistics Biorxiv



Pnumtzapcrtzcm



Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes



The Factors Of X 2 4y 2 4y 4x Y 2x 8 Are A X 2y 4 X 2y 2 B X Y 2 X 4y 4 C Youtube
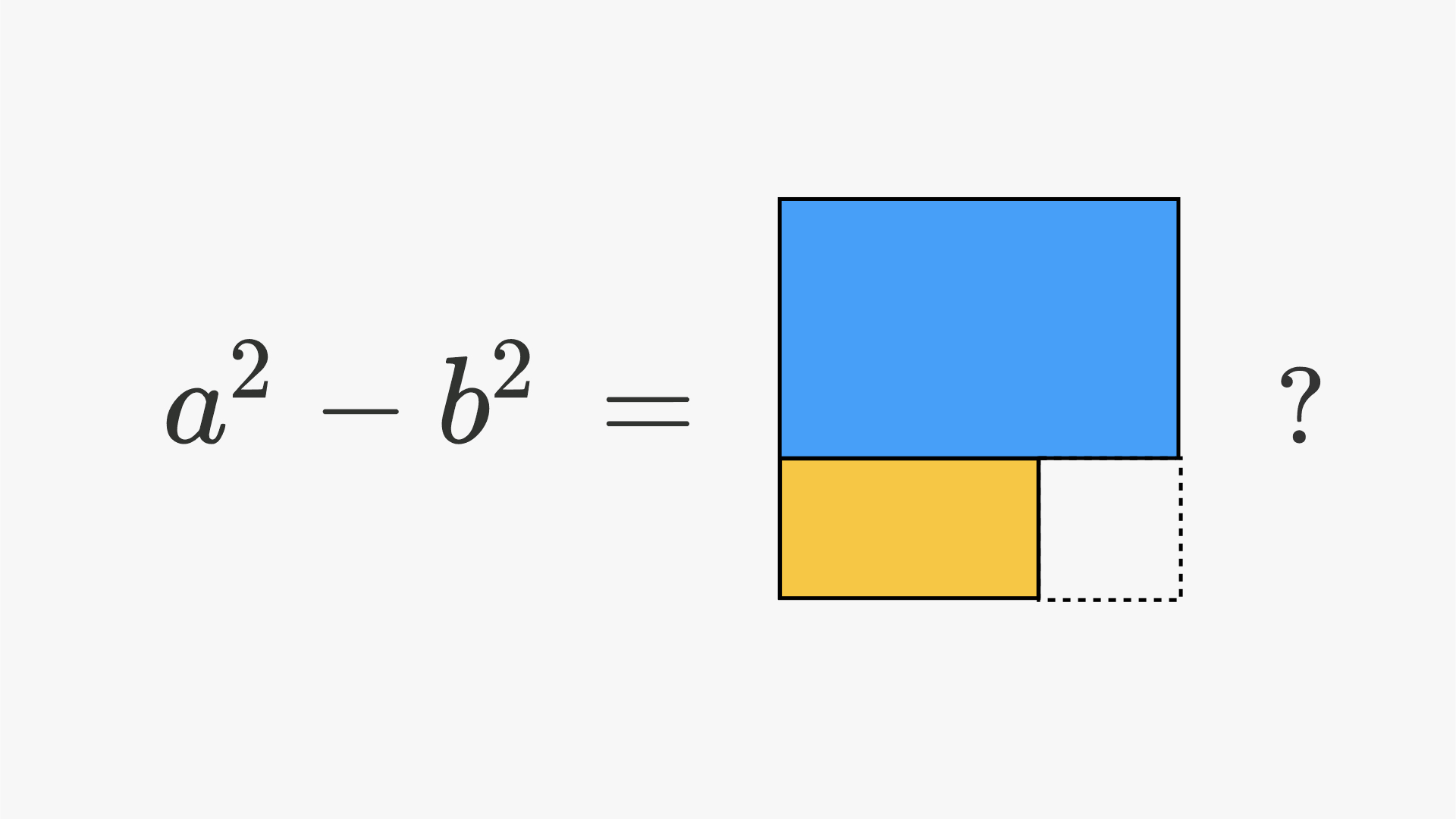


Difference Of Squares Brilliant Math Science Wiki



Ex 2 5 1 Class 9 Polynomials Use Suitable Identities To Find
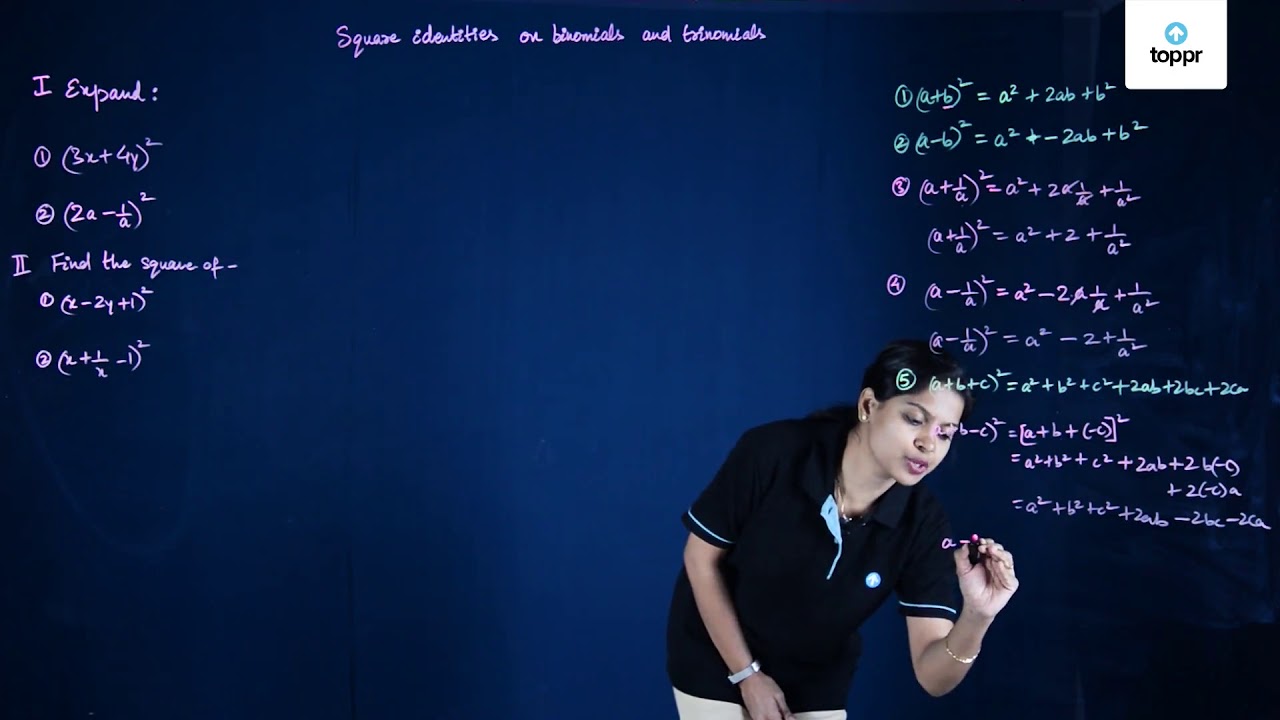


Standard Identities Of Binomials And Trinomials Equations Examples



Expand And Simplify Binomial Squares 2x 3y 2 Youtube



How To Factorise Using The Identity X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Youtube



Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes



2 X Square Y Square 8 Z Square 2 Root 2 X Y 4 Root 2 Y Z 8 X Z Brainly In



Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes



Expand Each Of The Following Using Suitable Identities I X 2y 4z 2 Ii 2x Y Z Youtube



The Binomial Theorem Explained With A Special Splash Of Pascal S By Brett Berry Math Hacks Medium



Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes



Factorise I 4x 2 9y 2 16 Z 2 12 X Y 24 Y Z 16 X Z Ii 2x 2 Y 2 2sqrt 2 X Y 4sqrt 2 Y Youtube



Expand And Simplify Trinomial Square A B C 2 A 2 B 2 C 2 2ab 2ac 2bc Youtube



Expand 2x 3y 2z 2 Brainly In
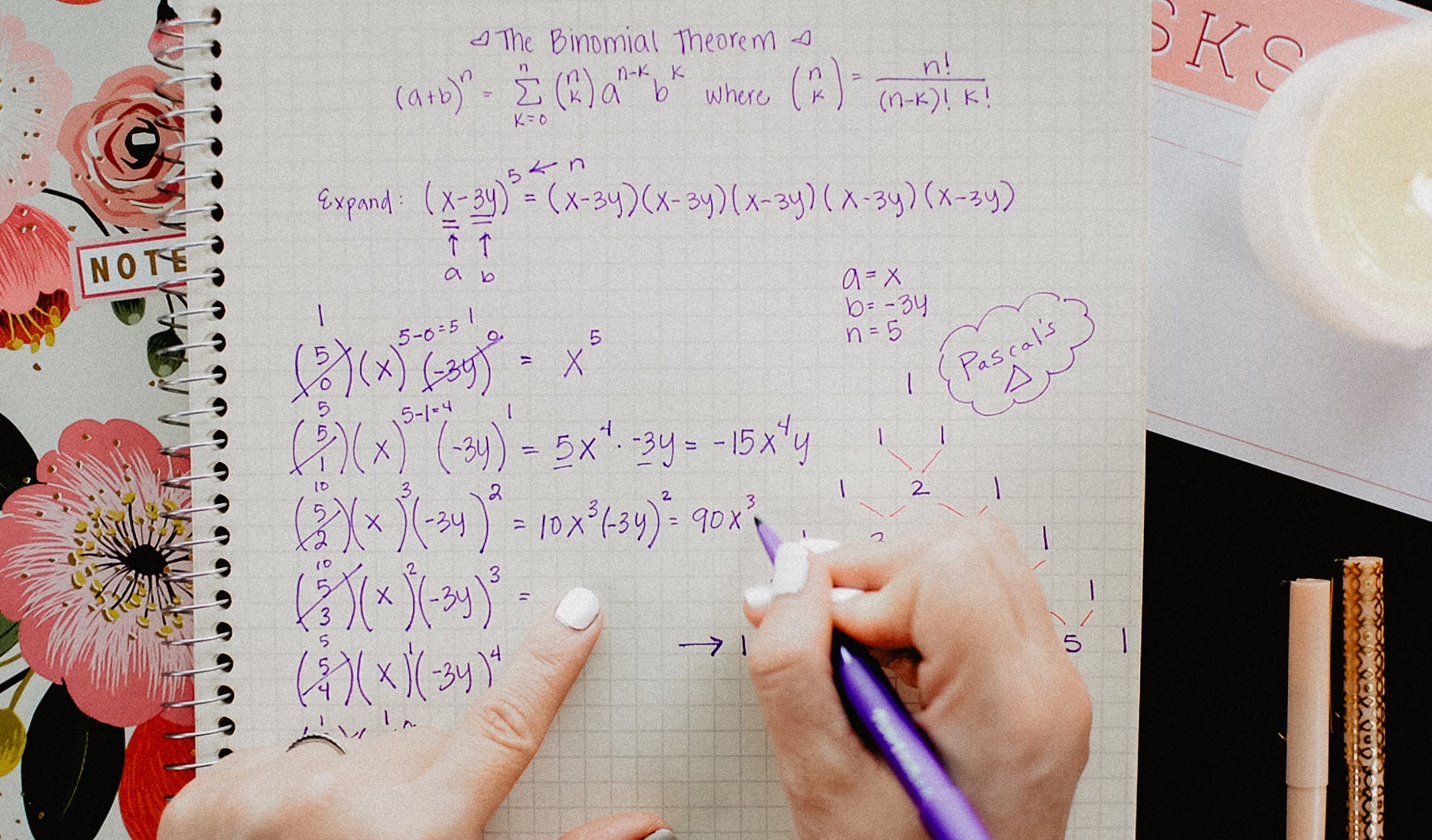


The Binomial Theorem Explained With A Special Splash Of Pascal S By Brett Berry Math Hacks Medium



Expanding Binomials W O Pascal S Triangle Video Khan Academy



Ex 2 5 4 Expand Each Of The Following Using Suitable
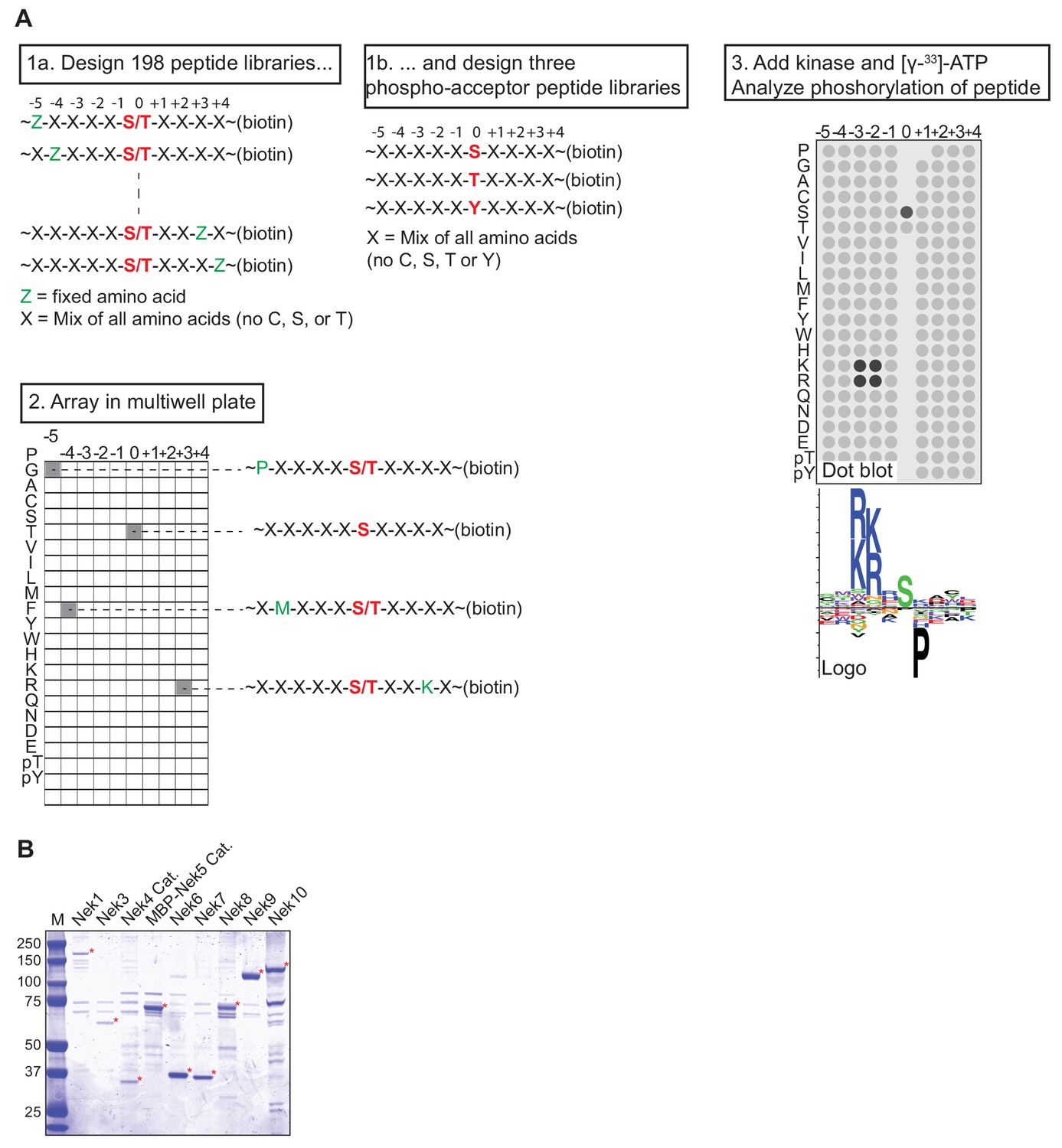


Comprehensive Substrate Specificity Profiling Of The Human Nek Kinome Reveals Unexpected Signaling Outputs Elife



Question 6 Write The Following Cubes In Expanded Form I 2x 1 3 Ii 2a 3b 3 Iii 3x 2 Brainly In



Evaluate The Following Using Suitable Identities I 99 2 Youtube



Ex 2 5 4 Expand Each Of The Following Using Suitable



Expand 2x 5y 3 By Using Suitable Identity Brainly In



Example 11 Using The Identity I Find I 2x 3y 2 Ii 103 2



Scalable And Isotropic Expansion Of Tissues With Simply Tunable Expansion Ratio Park 19 Advanced Science Wiley Online Library



Class 9 Polynomial 2 Coordinate Geometry Linear Equation In Two Variables Euclid S Geometry Lines And Angles Notes



Polynomial Identities Introduction Video Khan Academy



Swarm Eoportal Directory Satellite Missions



Complex Number Wikipedia



Direct Simulation Of Random Field Samples From Sparsely Measured Geotechnical Data With Consideration Of Uncertainty In Interpretation


Covid Economics Centre For Economic Policy Research



No comments:
Post a Comment